插入排序,一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中。
算法原理
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素小于序列中的元素,则比较下一个位置的元素
- 重复步骤3,直到找到序列中的元素小于或等于该元素的位置
- 将该元素插入到该位置
- 重复步骤2-5直到所有元素已排序
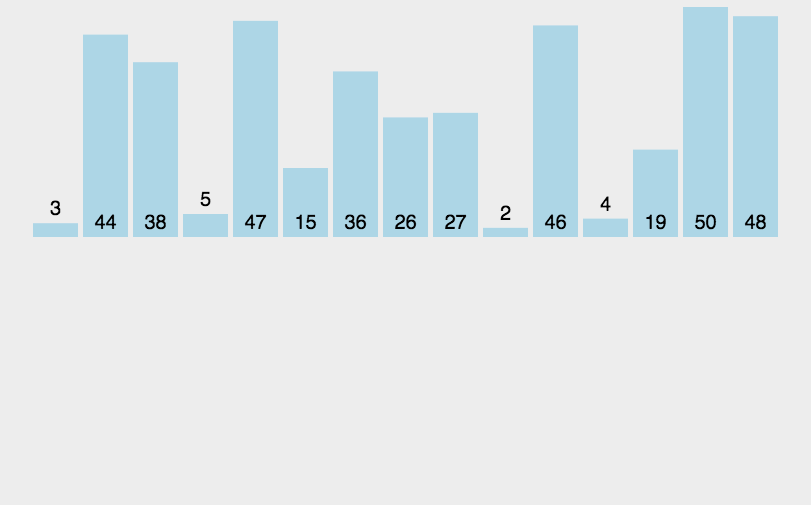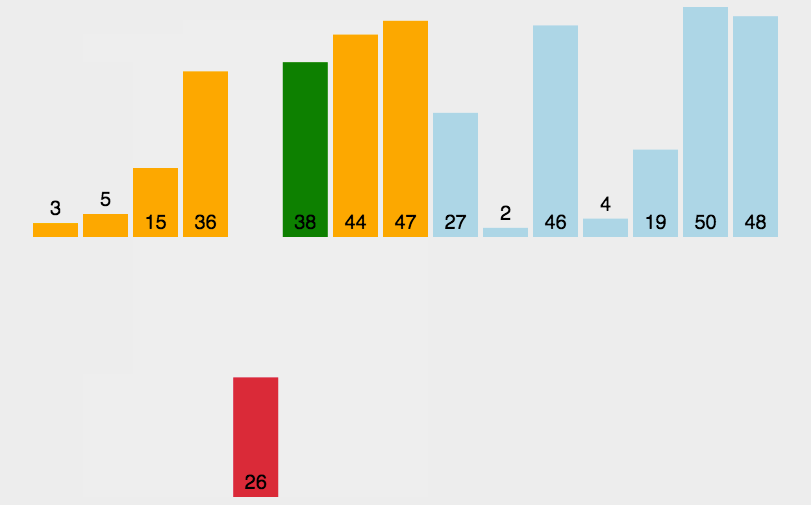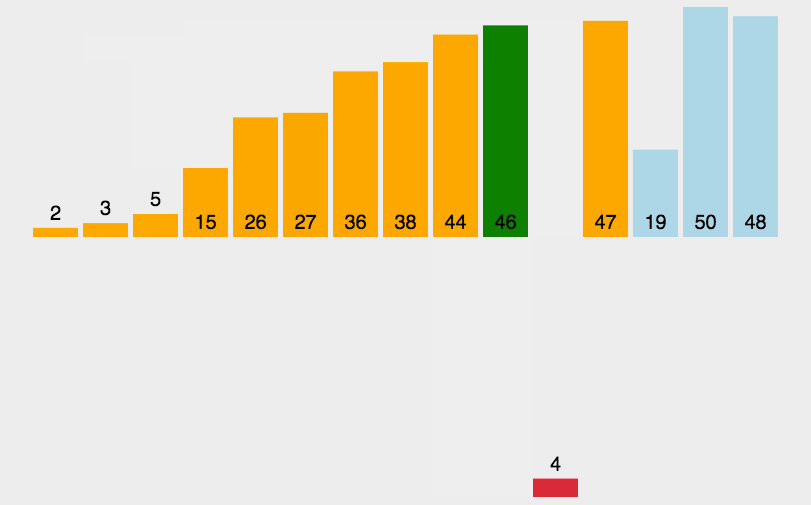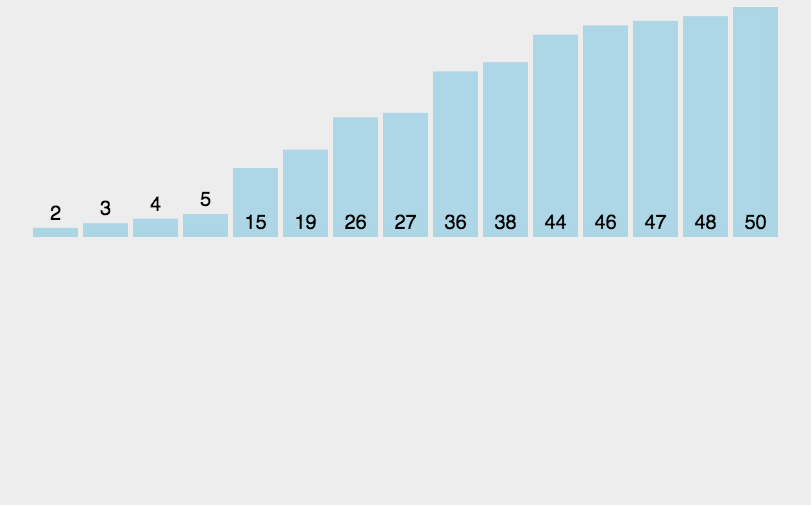
代码实现
l = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
# 1. 第一种写法
def insert_sort(ls):
for i in range(len(ls)-1): # n个元素的列表需要n-1次插入
next = ls.pop(i+1) # 取出未排好序的第一个元素
length = i+1 # 已排序序列的长度
# 从后往期,依次比较未排序元素与排好序元素的大小
for j in range(length):
if next >= ls[length-j-1]: # 如果next大于当前元素则不用继续往后比较
break
# length-j就是next应该插入的位置
ls.insert(length-j, next)
# 2. 第二种写法
def insert_sort(ls):
for i in range(1, len(ls)): # n个元素的列表需要n-1次插入
min_index = i # 记录当前位置为最小元素的索引
# 从后往期,依次比较未排序元素与排好序元素的大小
for j in range(i):
if ls[min_index] < ls[i-j-1]:
# 如果最小位置的元素小于比较位置的元素就相互交换
ls[min_index], ls[i-j-1] = ls[i-j-1], ls[min_index]
# 并记录最小索引为当前位置
min_index = i-j-1
else:
break
# 3. 第三种写法
def insert_sort(ls):
# 长度为n的列表需要n-1轮插入排序
for i in range(1, len(ls)):
# 当前未排序元素的索引
cur_index = i
# 前一个待比较的元素的索引
pre_index = i - 1
while pre_index >= 0:
if ls[cur_index] > ls[pre_index]:
break
else:
# 如果当前元素小于前一个元素则交换位置
ls[cur_index], ls[pre_index] = ls[pre_index], ls[cur_index]
# 修改待排序元素索引
cur_index = pre_index
# 计算下一个元素索引
pre_index -= 1
insert_sort(l)
print(l)
运行结果:
[3, 2, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
分析总结
1. 时间复杂度
- 在插入排序中,当待排序数组是有序时,是最优情况,只需当前数跟前一个数比较一下就可以了,这时一共需要比较N-1次,时间复杂度为O(N).
- 最坏的情况是待排序数组是逆序,此时需要比较次数最多,总次数计为:1+2+3+....+N-1,所以,插入排序最坏情况下的时间复杂度为

- 平均来说,A[1...j-1]中的一般元素小于A[j],一半元素大于A[j]。插入排序在平均情况运行时间与最坏情况运行时间一样,是输入规模的二次函数。
2.空间复杂度
在插入算法过程中,临时占用存储空间大小不变,空复杂度为O(1)
3.稳定性分析
根据算法原理,当序列中有两个相同的元素,排序后他们的相对位置保持不变啊,因此插入算法是稳定的。
4. 应用分析
插入排序适用于已经部分数据已排好,并且排好的部分越大越好。一般在输入规模大于1000的场合不建议使用插入排序。
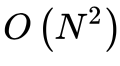
欢迎来到testingpai.com!
注册 关于