一、算法原理
归并排序是一种典型的分治算法,它由约翰·冯·诺依曼于1954年发明,至今仍被广泛使用。和多数分治算法一样,用递归方式描述它是最容易的:
- 如果列表的长度是0或是1,那么它已经排好序了;
- 如果列表包含多于1个元素,那就将其分成两个列表,并分别使用归并排序进行排序;
- 合并结果。
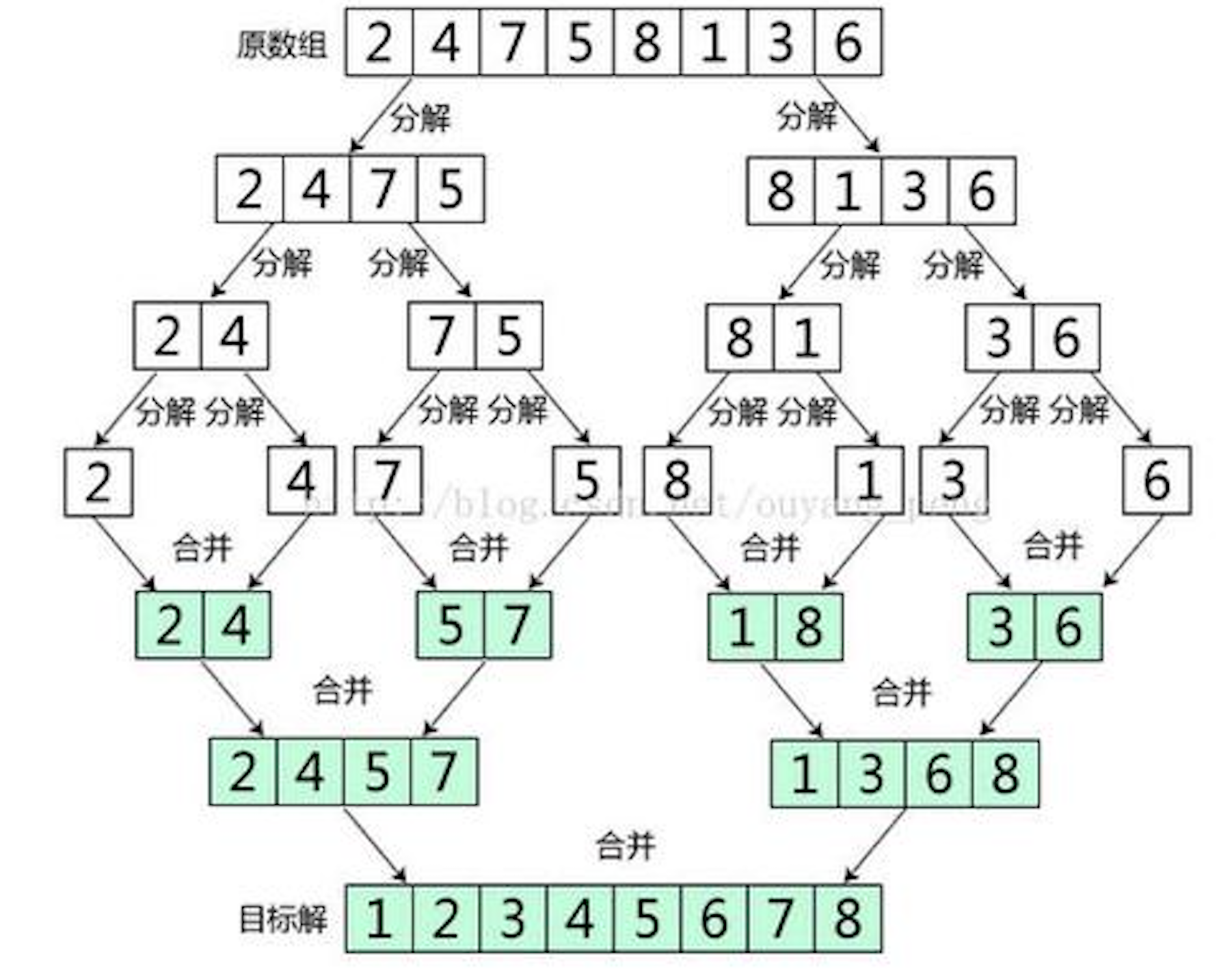
冯诺依曼的关键发现在于,两个有序的列表可以高效的合并成一个有序列表。合并的思想是,先看每个列表的第一个元素,然后将二者较小的一个移动到目标列表的末尾。其中一个列表为空时,就将另一个列表中余下元素复制到目标列表的末尾。
合并过程的复杂度是多少呢?过程中有两个常数时间操作,比较元素的值和从一个列表向另一个列表复制元素。比较的次数是O(len(L)),这里的L是两个列表中较长的那个。复制操作的次数是O(len(L1))+O(len(L2)),因为每个元素正好复制一次。因此,合并两个有序列表的复杂度与列表的长度成线性关系。
二、归并排序算法实现
# !/usr/bin/env python
# -*- coding:utf-8 -*-
# create_time:
# Author = '心蓝'
def merge(left, right, compare):
"""
:param left: 有序列表
:param right: 有序列表
:param compare: 定了排序规则
:return: 有序列表
"""
result = []
i, j = 0, 0
while i < len(left) and j < len(right):
if compare(left[i], right[j]):
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
while i < len(left):
result.append(left[i])
i += 1
while j < len(right):
result.append(right[j])
j += 1
return result
def merge_sort(L, compare=lambda x, y: x < y):
"""
归并排序
:param L: 一个无序的列表
:param compare: 排序规则
:return: 有序的列表
"""
if len(L) < 2:
return L
else:
middle = len(L)//2
left = merge_sort(L[:middle], compare)
right = merge_sort(L[middle:], compare)
return merge(left, right, compare)
if __name__ == '__main__':
import random
l = [random.randint(1, 1000) for _ in range(10)]
print(l)
print(merge_sort(l))
print(l)
运行结果:
[504, 573, 546, 324, 961, 439, 113, 10, 394, 564]
[10, 113, 324, 394, 439, 504, 546, 564, 573, 961]
[504, 573, 546, 324, 961, 439, 113, 10, 394, 564]
欢迎来到testingpai.com!
注册 关于